通过从n个不同的项目中选择r个项目来计算组合总数。
组合计算
关于组合的计算
输入总数(n)和所选数(r),然后单击“计算组合”按钮,计算并显示组合总数,以便从 n 项中选择 r 项且不重复。
它还展示了如何计算组合总数。
请输入 总数 和 选定的号码 作为正整数,最多为 10,000。
什么是组合?
组合是对几种可以区分的不同事物的选择。
组合总数写为nCr,表示从总数(n)中选出的数(r)的组合总数。
nCr = 从n项中选择r项时的组合总数
例如,假设您从四个字母 A、B、C 和 D 中选择了三个。
此时有四种方式可供选择:ABC、ABD、ACD、BCD。
与排列不同的是,组合不考虑顺序,因此像ABC、CBA这样的组合,重新排列后相同的就被认为是一个。
如果您从 A、B、C 和 D 中选择三个,则组合在树状图中将如下所示。
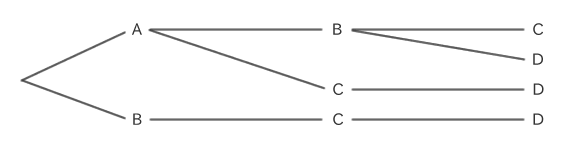
如何计算组合
要计算组合总数,请将组合总数除以相同组合的数量。
例如,假设有四个字母:A、B、C 和 D,您想选择其中三个并想出一个组合。
排列总数为 4 x 3 x 2,即 24 种排列方式。
然而,在排列时,“ABC、ACB、BAC、BCA、CAB、CBA”这六种排列方式由于没有考虑顺序,组合起来就变成只有一种方式。
因此,排列总数 (24) 除以 6 得出 4 种组合。
唯一相同的组合是所选数字的排列,因此如果您选择 3,3! 将产生 6 种方式。
因此,从n个项目中选择r个项目的组合总数可以计算为nPrr!。
另外,由于它是 nPr = n!(n−r)!,因此它变为 nPrr! = n!(n−r)! × 1r! = n!r!(n−r)!。
组合总数的公式
nCr = nPrr!
nCr = n!r!(n−r)!
此外,从 n 个项目中选择 r 个项目与不从 n 个项目中选择剩余的 (n−r) 个项目相同。
因此,选择r项的组合总数和选择(n−r)项的组合总数相同,且nCr和nC(n−r) 相等。
nCr = nC(n−r)