通过允许 重复 并从 n 个不同的项目中选择 r 个项目来计算组合总数。
组合计算(有重复)
关于组合计算(有重复)
输入总数(n)和选择的个数(r),点击“计算组合”按钮,允许重复,从n个中选择r个,计算并显示要提取的组合总数。 。
它还展示了如何计算组合总数。
请输入 总数 和 选定的号码 作为正整数,最多为 10,000。
什么是重复组合?
组合是对几种可以区分的不同事物的选择。
通过允许 重复 选择的组合称为 组合。
例如,假设您从三个字母 A、B 和 C 中选择两个。
您可以多次选择同一项目,因此有 6 种选择方式:AA、AB、AC、BB、BC、CC。
与排列不同,组合不考虑顺序,因此AB、BA等重新排列后相同的组合被视为1。
如果从 A、B 和 C 中选择两个并制作组合的树状图,它将如下所示。
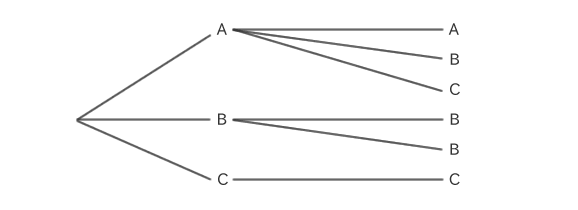
如何计算重复组合
计算 重复组合 的总数时,请考虑使用圆圈和分隔线。
例如,假设有 A、B 和 C 三个字母,您想选择其中四个并想出一个组合。
将可供选择的四种字母圈起来(〇),由于字母有三种,所以准备两个分隔物(|)并将它们排成一行。
将圆和分隔线对齐,并从分隔线的左侧将其称为 ABC。
例如,〇〇|〇|〇是AABC的组合。另外,在〇||〇〇〇的情况下,它是ACCC的组合。
该圆和分隔线的排列总数是重复组合的总数。
圆和分区的排列总数为6!,并且圆和分区之间没有区别,因此除以(4!×2!)。
因此,组合总数为6!4!2! = 15。
因此,从n个允许重复的项目中选择r个项目提取的组合总数可以计算为(r+n−1)!r!(n−1)!。
重复组合总数的公式
n+r−1Cr = (r+n−1)!r!(n−1)!